Дифференциальные уравнения, описывающие процессы в цепях с сосредоточенными параметрами.

При работе электрических цепей используются два закона Кирхгофа. Рассмотрим их в применении к цепи с сосредоточенными параметрами.

Первый закон Кирхгофа

применяется к узлам электрической цепи. Он вытекает из принципа непрерывности электрического тока. Охватим узел цепи замкнутой поверхностью S (рис.)

В соответствии с принятыми допущениями вся электрическая ёмкость в цепи с сосредоточенными параметрами предполагается сосредоточенной в конденсаторах, включённых в цепь. Это соответствует пренебрежению токами электрического смещения, отходящими от соединительных проводов к другим участкам цепи. Таким образом, через замкнутую поверхность S проходят только токи проводимости в проводниках, пересекающих эту поверхность. Согласно принципу непрерывности тока в данном случае получим:

- сумма токов всех родов проводимости, смещения сквозь любую замкнутую поверхность равна нулю.

-плотность тока

При любом числе ветвей имеем: 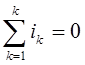, т.е. алгебраическая сумма токов, расходящихся от узла электрической цепи, равна нулю.

При составлении уравнений согласно І закону Кирхгофа необходимо задаться условными положительными направлениями токов во всех ветвях, обозначив их на схеме стрелками. От узла, как правило, принимаем за положительное направление для токов, а знак «минус» приписываем токам, которые входят в узел. Для случая на рис. перед всеми токами в уравнении следует поставить знак «плюс».

: -i1 + i2 + i3 = 0

Если в результате расчёта будет получено для некоторого тока в некоторый момент времени положительное число (ik > 0), то это значит, что ток имеет в данный момент времени действительное направление согласно стрелок. Если же будет получено ik < 0, то этот ток в действительности направлен против стрелки.

Второй закон Кирхгофа

применяется к контурам электрической цепи. Он вытекает из соотношения:

ЭДС, действующая вдоль некоторого пути, равна линейному интегралу вдоль этого пути напряжённости стороннего электрического поля, а также электрического поля, индуктированного изменяющимся магнитным полем.

Электрическое напряжение или падение напряжения связано с результирующим электрическим полем.

Электрическое напряжение вдоль некоторого пути от (·) А до (·) В равно линейному интегралу напряжённости результирующего электрического поля (электростатического, стороннего, индуктированного) вдоль этого пути.

Величина равна сумме ЭДС.

источников сторонних ЭДС, действующих в контуре.