Дифференциальные уравнения движения системы и их интегрирование

Составим уравнения движения с помощью уравнений Лагранжа 2-го рода. В выбранных обобщенных координатах и они принимают вид:

(2.1.1)

где - кинетическая энергия системы;

png">- обобщенные силы, соответствующие обобщенным координатам и .

Найдем кинетическую энергию системы. Она состоит из кинетических энергий всех тел, входящих в систему:

Абсолютная скорость шарика равна геометрической сумме относительной и переносной скоростей (см. рис. 3), ее величина определяется по формуле:

Тогда для кинетической энергии системы получим:

(2.1.2)

Введем обозначения:

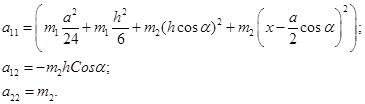
Найдем все производные левой части уравнений (2.1.3):

Обобщенные силы можно определить двумя способами:

1. Фиксируем координату , даем виртуальное перемещение , находим элементарную работу:

Фиксируем координату , даем виртуальное перемещение , находим элементарную работу:

2. Вычислим потенциальную энергию системы:

Найдем обобщенные силы:

Подставив производные левой части уравнений (2.1.1) и обобщенные силы и в уравнения (2.1.1), получим дифференциальные уравнения движения системы:

Для решения системы дифференциальных уравнений движения механической системы проведем численное интегрирование на ЭВМ. Результаты численного интегрирования приведены в приложении №2.